4. The remarkable history and properties of the Golden b
As we have already seen, the Golden b is a fascinating shape with some very interesting properties. But there is a lot more to its story than just Fibonacci numbers and the golden ratio.
Let’s take a short tour through the history of the Golden b to discover some more of its unique properties.
Tilings and the discovery of the Golden b
In geometry, a tiling (or tessellation) refers to covering a plane with shapes (called tiles) in a way that means there are no gaps or overlaps.
You have seen plenty of tilings in the real world, such as on your kitchen floor or bathroom walls. These ‘real world’ tilings are usually what we call periodic tilings – even if they contain several different shapes of tiles, those tiles are arranged to fill the plane (i.e. the wall or the floor) in a relatively simple repeating pattern.
Here are some examples of periodic tilings:

By Tomruen (Own work) [CC BY-SA 4.0], via Wikimedia Commons

By Tomruen (Own work) [CC BY-SA 4.0], via Wikimedia Commons

By Tomruen (Own work) [CC BY-SA 4.0], via Wikimedia Commons

By Tomruen at English Wikipedia [Public domain], via Wikimedia Commons
However, there are also aperiodic tilings – tilings that do not repeat in any regularly, evenly spaced way. The first aperiodic tiling was discovered by the logician Hao Wang in 1961, and throughout the 1960s and 70s, several mathematicians were collaborating and competing to find small, elegant sets of aperiodic tiles – shapes that can tile a plane non-periodically when used together and following certain rules.
In 1976, Scientific American magazine announced that the renowned mathematician Roger Penrose had discovered a set of just two tiles that could tile a plane aperiodically. Unfortunately, Penrose wasn’t going to tell anyone what they looked like until he received a patent for them. Nevertheless, it was huge news among the mathematical community.
But the following year, a man called Robert Ammann wrote to Scientific American describing a set of two aperiodic tiles that he had discovered. Martin Gardner, the Scientific American journalist who had broken the news of Penrose’s discovery, was confused – he knew every single mathematician working on tiling, and none of them were called Robert Amman. It turned out Ammann wasn’t a professional mathematician at all – he was a university dropout who worked as a mail snfor the US Post Office and investigated tiling theory in his spare time!
Some of Ammann’s tiles turned out to be identical to one of Roger Penrose’s sets, while others were very similar, but not identical, to the Golden b.
Robert Ammann went on to discover several more sets of aperiodic tiles, including the shape we now call the Golden b.
In 1986, the shape made it’s official debut in the book Tilings and Patterns, the so-called ‘bible of tilings’.

Aperiodic tiling of Golden b shapes
Polygons, rep-tiles and the New Zealand connection
The next person to discover one of the Golden b’s unique properties was a German-born New Zealander named Karl Scherer. Scherer was also the first person to call the shape a golden b (or ‘bee’) because of its resemblance to a lower-case b and its relation to the golden ratio.
Like Robert Ammann, Karl Scherer was not a professional mathematician – he was a software engineer with an interest in polygons.
Polygons are shapes made up entirely of straight edges. Triangles and squares are polygons. So are rectangles, pentagons and, of course, Golden bs.
Certain polygons can be divided into smaller polygons, each of which is a smaller version of the original shape (in mathematical terms, they are ‘similar’). Polygons that can be divided this way are called rep-tiles.
For example, a square is a rep-tile, because it can easily be divided into four equally-sized smaller squares:

If the smaller shapes making up a rep-tile are not all the same size, the polygon is known as an irregular rep-tile, or irreptile.
A lot of polygons are rep-tiles. But Karl Scherer noticed that there only seem to be a few rep-tiles that contain just two smaller copies of themselves – all the others are made up of more than two copies. Those shapes are:
- a right-angled triangle (irreptile as long as the sides are all of different lengths)
- a parallelogram with sides in the ratio of `1:1/sqrt(2)`
- the golden b (also an irreptile).
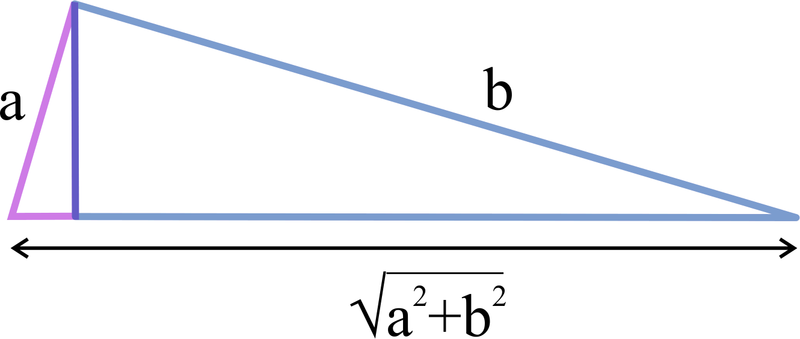
A right-angled triangle is made up of two similar right-angled triangles. As long as all sides of the triangle are different lengths (i.e. it is not an isosceles triangle), the triangle is also an irreptile, because the two smaller triangles are different sizes.
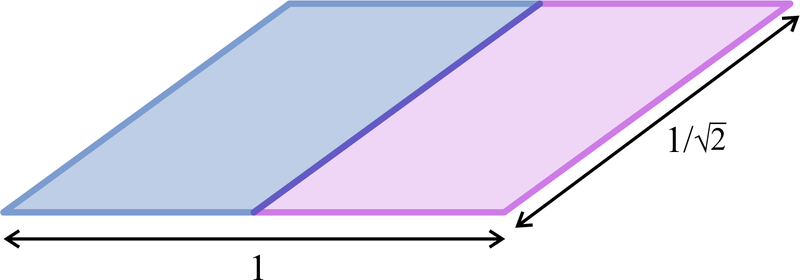
A parallelogram with sides in the ratio `1:1/sqrt(2)` can be split into two smaller parallelograms of the same size.

A Golden b can be split into two smaller Golden bs. Because these smaller bs are different sizes, the Golden b is an irreptile.
In 1987, Scherer conjectured that these three shapes are the only polygons that can be subdivided into two smaller copies of themselves.
But it wasn’t until 2011 that James Schmerl at the University of Connecticut fully proved Karl Scherer’s conjecture, showing that there are no other polygons that can be divided into two similar pieces.
So there you have it – as well as having the golden ratio and Fibonacci sequence embedded in its dimensions, the Golden b is:
- one of the few shapes that can be used for aperiodic tiling
- one of only three polygons that can be divided into two smaller copies of itself
- the only rectilinear (i.e. right-angled) polygon where the two smaller copies are different sizes
Next we’ll discover how the Golden b is related to certain special fractals.
Unlock more mathematical discoveries
Get a Golden b Puzzle and start exploring.