3. Why is the Golden b ‘golden’?

The Golden b shape has the golden ratio (`phi = (1 + sqrt(5))/2`) embedded into its size and shape. To find out where, let’s start by examining two interlocking Golden b tiles:

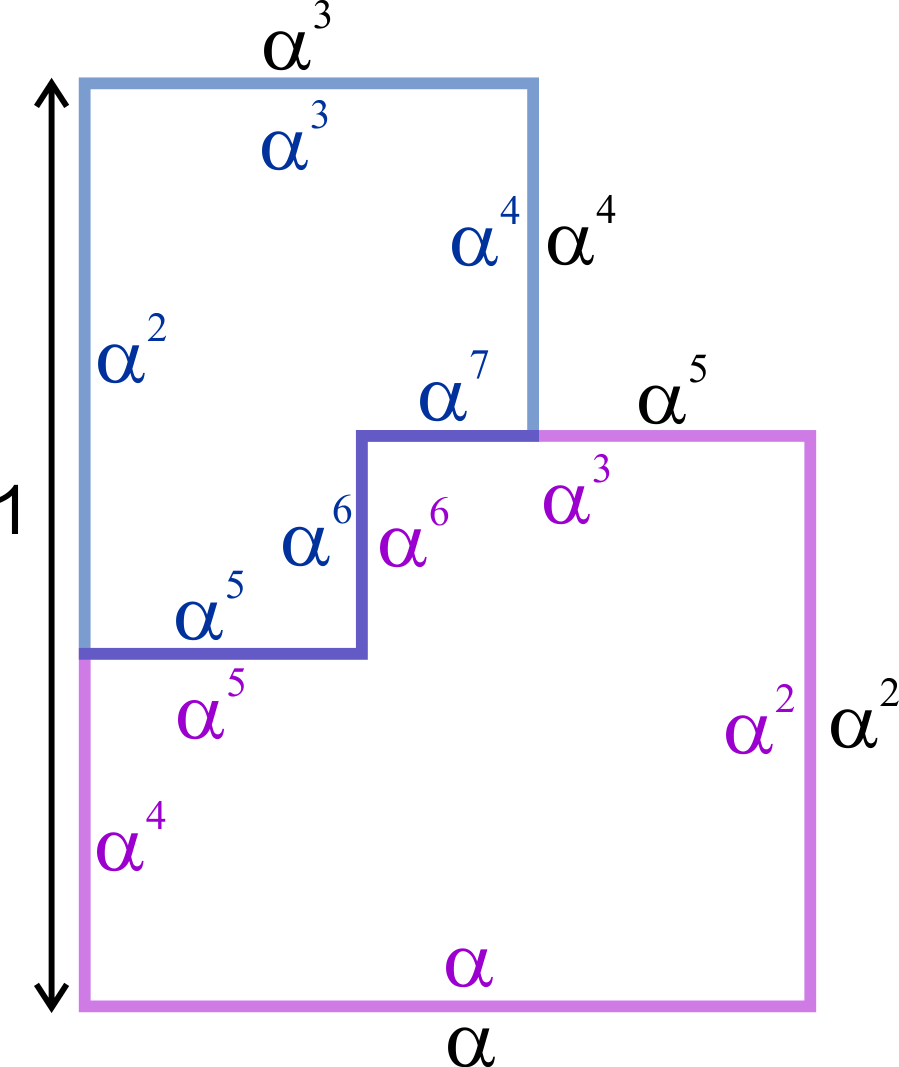
One of the properties of the Golden b is that the length of each side is just the length of the next longest side multiplied by a constant factor. Let’s call this factor `alpha`, and assume for the moment that we don’t know what it is.

In the diagram above, we’ve given the longest side of the combined b-shape a length of 1. That means the second-longest side of the combined b (i.e. the longest edge of the purple b-tile) will have a length of `1 * alpha = alpha`.

Following this same pattern, the second-longest edge of the purple tile is simply the longest edge of the purple tile multiplied by `alpha`, or `alpha * alpha = alpha^2`.

The next shortest side is `alpha * alpha^2 = alpha^3`.

And so on, all the way down to the shortest side of the purple tile, which has a length of `alpha^6`.

This shortest side of the purple tile is the same size as the second-shortest side of the smaller blue tile. Therefore, the second-shortest side of the blue tile is also `alpha^6` long.

That means the shortest side of the blue b-tile is `alpha^7` long, and the third-shortest side is `alpha^5`. Following this process, we discover that the longest side of the blue tile is `alpha^2`.

Now, because the longest side of the combined b has a length of 1, we know that:

`alpha^4 + alpha^2 = 1`

This is actually a quadratic equation we can use to find the value of `alpha`.

If we let `x = alpha^2`, we can rewrite the equation as:

`x^2 + x -1 = 0`

We can then solve this for x  using the quadratic formula:

`x=(-b +- sqrt(b^2-4ac))/(2a)`, with `a = 1`, `b = 1` and `c = -1`.

This formula gives us the solutions:

`x= (+-sqrt(5)-1)/2`

We ignore the solution that would give us a negative value for x, and stick with:

`x= (sqrt(5)-1)/2`

You might notice that this is very similar to the value of the golden ratio: `phi = (1 + sqrt(5))/2`.

By multiplying the top and bottom of our solution by `(sqrt(5)+1)`, we get:

`x=((sqrt(5)-1)(sqrt(5)+1))/(2(sqrt(5)+1))`

And because `(sqrt(5)-1)(sqrt(5)+1)=5-1=4`, we can simplify this to:

`x = 4/(2(sqrt(5)+1))`

And then to:

`x = 2/((sqrt(5)+1))`, which is the same as `1/phi`, where `phi` is the golden ratio!

Remembering that `x = alpha^2`, we can finally calculate the value for our constant `alpha`:

`alpha = sqrt(x) = 1/sqrt(phi)`

Therefore, the ratio between the length of one side of a Golden b tile and the next longest side is `1/sqrt(phi)`, or approximately 0.78615.

So now you know where the golden ratio is hiding in the Golden b!

Next, let’s take a look at some more of the Golden b’s interesting properties.